the blue blog archives: hexagons, or the six-sided math problem

After writing about the patchwork hexagon throw on the cover of Erika Knight's new book, Classic Knits at Home, last week, I had to start knitting hexagons. What a great project for using up some of the yarns I have in my core stash (that untouched core stash of yarns I bought ages ago for some sweater I never knit, but have never been able to part with)! First up out of the core stash, some GGH Via Mala in chocolate brown (coming soon, this same yarn in pale pink and beige - good colors for a blanket, right?).

Hexagon number one is in double moss stitch and number two is in a stockinette/garter stripe. Love that effect on the second one!

What I really loved about this pattern is its mixture of knitting and fabric. I've already pulled out these old sweaters from the closet to use for at least some of the "fabric" hexagons.

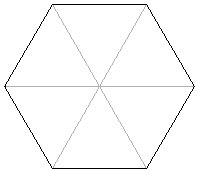
I haven't decided if I want to felt them or not. I'm not even sure all of them will felt. And I'm not averse to steeking them. That way they'll have the same knitted look as the hexagons I'm knitting now. A throw that will use up stash yarns and old sweaters?! This... is... AWESOME!

Except for the math. So here's the math problem: how do you measure a hexagon? Erika Knight, rather unhelpfully, gives the hexagons' proper measurement as 7" x 7". Um, that's not enough sides. It's not a square. It's not even an octagon that fits neatly into a square. It's a regular hexagon, with each side the same length, meaning that it is wider at its widest point than it is tall (uhhh, something about it being made from equilateral triangles and the hypotenuse being longer than the height of the two right triangles in each triangle, blah, blah, math, math...).

So what could the two equal measurements she gives refer to? A hexagon fits into a circle, soooo is the 7" the diagonal line between each of the points (or what would be the diameter of the circle that fits around the hexagon)? Then why give two measurements? In quilting, a hexagon's size is usually described by just one measurement: the length of each side. I'm confused.

Look, all I need to know is what size should my hexagons be? I'll be using different yarns, so I need to have some idea of what size things should be. Her gauge info is, again rather disappointingly, no help since she only gives one gauge and that's in stockinette stitch, whereas all the hexagons are done in a variety of different stitch patterns from seed stitch to ribbing and even a cable! And I need to know what size should I cut my sweater hexagons.

posted by alison at 10:27 am | in patchwork hexagons

Comments

If I'm writing a hexagon pattern (and I, oddly enough, have been lately) I would make the hexagon measurement 7" point-to-point. Maybe that's what she means?

I'm surprised by this though. Erika Knight's patterns are usually quite good.

I love this new hexagon trend. They're so much more visually interesting than squares. I need to finish my hexagon blankie, it's so close to being done!

Posted by: nipper jenn at January 31, 2008 10:59 AM

How frustrating! That's clearly an oversight in the pattern--you're right in that the hexagons are regular ones, with all sides being equivalent, as seen in the cover photo in the hexagons resting on the back of the couch.

Does Erika Knight give the dimensions of the finished throw? If so, you could add up the lengths of the sides and the point-to-point distances (i.e., twice the length of each side) for the total number of hexagons on one side of the pattern to see if your total length matches that of the instructions.

I agree with Jenn that the 7" measurement is probably the point-to-point value, in which case you'll want to knit/cut hexagons that have 3.5"-long sides and a height (the flat side-to-flat-side distance) of approx. 6".

Posted by: Andrea at January 31, 2008 11:24 AM

Love the colors! I just can't believe that after sewing all those blocks together at Christmas time, that you are ready to do that again! Ü I made the rambling rows afghan this past year. I love how those blocks just build on each other. Is there any way to start a new block off an existing one so you don't have to sew so much? (I know, you probably really enjoy that sewing.)

Posted by: Marcia at January 31, 2008 11:28 AM

What size are your current hexagons? If you knit them as she called for - just make sure the rest of the hexagons are that size. If they are slighty different then 7" but all of yours are the same. It will still turn out - this is a blanket after all. With a sweater I wouldn't be so cavelier.

If one side is 7", the distance across is 12.12" and from point to point is 14".

Posted by: Teresa at January 31, 2008 11:38 AM

That's not pop you're cutting, right?

As for hexagons and measurements, I'm not sure. Maybe check the publishers website, and see if they have any errata/helpful hints. You could always write them and see whether they can reach out to Erika as well. That's frustrating that they don't help on that.

Posted by: Heather at January 31, 2008 11:48 AM

You're putting too much into it. Make it the size you want and don't worry about what size it's 'supposed' to be. Then make all your hexagons the same size as each other.

Posted by: Carol at January 31, 2008 11:50 AM

I was going to say "do it how you like it" but Carol beat me to it. :D As long as they're the same size, it shouldn't matter.

Posted by: ames at January 31, 2008 12:13 PM

It seems to me that she might just mean the length of one side & thought that was the most succinct way to say it. I agree - just make them the size you want them to be. I'd go for larger rather than smaller (in part because it would require fewer but I also just think it would look better).

Posted by: Donna at January 31, 2008 12:19 PM

It's wider at its widest point than it is tall?! I was tempted to grab the ruler and measure the hexagon on the screen, but then I remembered how much I dislike math and decided I'd take your word for it. But maybe Erika doesn't know that!

Posted by: Suzanne V. (Yarnhog) at January 31, 2008 2:20 PM

(uhhh, something about it being made from equilateral triangles and the hypotenuse being longer than the height of the two right triangles in each triangle, blah, blah, math, math...).

I found this line to be hysterical!

Posted by: Wanett at January 31, 2008 3:14 PM

Love the colors! It will be a beautiful afghan. I love the idea of using up old sweaters too. I can't wait to see more hexagons....and the finished product!

As for the size of the hexagon, I don't think it really makes much difference. Draw a hexagon (or use those ones you've knit already), and make yourself a template out of cardboard. Then just make em all the same size! I think it will turn out great no matter what you do.

Posted by: Kassia at January 31, 2008 5:08 PM

In the old days we would simply have measured from one end to the other right about the middle, but you really must follow your muse. Was there a knitting muse? Anyway, I think the completed ones are fab.

Posted by: Melissa at January 31, 2008 8:17 PM

Maybe she's just relying on the stretchiness of knitting to even things out.

Posted by: Andrea at January 31, 2008 10:39 PM

As a math challenged person, I can't help. I can just side on the sidelines and watch.

I can tell you how to knit a toilet paper cozy, though. It was supposed to be DBH (Dear Balding Husband's) hat. Now it's a hat for toilet paper.

Good luck, Alison. Be sure to let us know how it all turns out.

And btw, all that link to the mitered squares afghan did was make me long for more baby pics.

Posted by: Anita at February 1, 2008 12:03 AM

As the other Carol said, just decide how you are going to measure the 7" and make them all the same...

Posted by: Carol at February 1, 2008 10:48 AM

I'm totally clueless about the measurement of the hexagons, but I can tell you a math joke!

(I apologize in advance if I offend any Native Americans)

There were three Indian squaws. One slept on a deer skin, one slept on an elk skin, and the third slept on a hippopotomus skin. They all became pregnant and the first two each gave birth to a baby boy. The one who slept on the hippopotomus skin gave birth to twin boys. This goes to prove that the squaw of the hippopotomus is equal to sons of the squaws of the other two hides.

Pythagorean's theorum: In a right triangle, the square of the hypoteneuse is equal to the sum of the squares of the other two sides. (But you knew that!)

Posted by: Barbara at February 2, 2008 4:16 PM

wow! beautiful blanket... all the sewing together of the hexagons - it makes me a little light-headed!

Posted by: rebecca at February 4, 2008 11:48 AM