the blue blog archives: morning math

When I drop my boys off at school, there's always the schedule for the day written on the board in their classroom. There's music and gym, word work, and sometimes morning math. Are you ready for a little hexagon math in the morning?

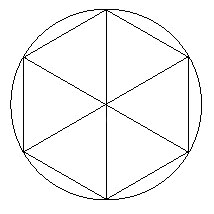
I spent some more time over the weekend trying to calculate the proper size of the hexagons in Erika Knight's patchwork throw from her new book, Classic Knits at Home. You might remember from last week that as I began making hexagons for the throw, I was puzzled as to what size they should be. Erika Knight gives the finished size of each hexagon at 7" x 7", which really doesn't make sense for a six-sided figure.

We left off our mathematical musings by noting that a regular hexagon is made up of six equilateral triangles and fits perfectly inside a circle (and not inside a square). At knitsmiths over the weekend, knitbuddy Carol took a few minutes to tackle the hexagon puzzle with me and realized that the length of each side of the hexagon would have to be equal to half the length of hexagon at its widest point. She didn't use exactly these words, but here's the gist: the length of the hexagon at its widest point is actually the same measurement as the diameter of the circle that the hexagon would fit into. Half of that length is the radius of that circle and that's one side of each triangle in the hexagon. And since they're equilateral triangles, the side of the hexagon must equal the length of that radius. With me so far?

If I crudely color in a couple of the triangles you can see that the widest point of the hexagon is the same length as two triangles and one side of the hexagon is the same length as one triangle. Fun, huh?

ignore the numbers in the diagram please, they're for the pattern not our math problem!

If we then look at the diagram of the throw, we see that the width of the throw is equal to 4 hexagon diameters plus 3 hexagon sides. Since the hexagon diameter is equal to twice the side, the width of the throw is equal to 11 times the width of each hexagon side (8 + 3). Erika Knight gives the width of the throw at 45", so each hexagon side is (skip the calculator) a little more than 4". And the diameter of each hexagon is 8" (twice the length of the side).

And it's height? Easy peasy. Divide one of the equilateral triangles into a right triangle and apply the pythagorean theorem. 4 (the hypotenuse) squared = 2 (the base of the right triangle) squared minus the height squared. Meaning, the height is (I got my calculator) a little more than 3 1/2". Soooo, the hexagon is twice that high, or about 7" high. Is that the 7" that Erika Knight first gave us??!!?!! Whew, how reassuring to actually find that number somewhere! Although I can only find one 7" measurement and still have no idea what 7" x 7" could mean. Still, can we verify that 7" height somehow just to be sure? Yes.

According to our diagram, the throw is six hexagons high and should measure 45". 6 hexagons at a wee bit more than 7" each is pretty darn close to 45". I'll take it!

Okey dokey, I'll be making and blocking my hexagons to be 4" hexagons (that's 4" at each side) that measure 7" high and 8" wide. And I'll be cutting my fabric hexagons to those measurements plus a little seam allowance, of course. Don't we all feel better now?

hexagons blocking, unaware of and unperturbed by the confusion that surrounds them

posted by alison at 11:01 am | in patchwork hexagons

Comments

don't you know that the boys could have figured that out much easier (and faster) than you? just ask them next time

Posted by: lisa b at February 4, 2008 11:11 AM

You may be right, Lisa! The boys and all the first graders are actually doing a math unit now on quilts in order to learn about geometry and shapes. Isn't that cool?! :)

Posted by: ALISON at February 4, 2008 11:16 AM

I love the maths. Are you going to crochet any hexagons? That would add another great texture.

Posted by: Roo at February 4, 2008 11:19 AM

Being a math teacher I really love your calculations. Next time my students ask me the famous question ("Why on earth do we have to know this?") I know what to show them! Thank you and great job!

Posted by: kathinka at February 4, 2008 12:42 PM

My head hurts just from looking at all of that, but geometry never was my strong suit. Give me equations any day. But go you for figuring it out!

Posted by: Alexis at February 4, 2008 12:54 PM

I never loved math, but when I went back to college and took "math for liberal arts" I was able to write a paper on the geometry involved in quiltmaking. It was my favorite math project evah!

Posted by: beverly at February 4, 2008 1:13 PM

Oooh, oooh do share more, Beverly! And come back this week, cause I'll be doing some quilting math later!

Posted by: ALISON at February 4, 2008 1:15 PM

Um, I said that? You put it much better Alison.

Posted by: Carol at February 4, 2008 1:39 PM

HUH?:)

Posted by: Jeanie at February 4, 2008 2:07 PM

My head is spinning from all that math!

Does this mean that you block the squares (hexagons) before you sew them together? What happens if you block the whole blanket later?

Do you block the blanket each time you wash it? How do the fabric and knitted hexagons wash together? Do the knitted ones lose shape while the fabric ones shrink?

Posted by: Anita at February 4, 2008 2:59 PM

All good questions, Anita. I wish Erika Knight gave answers for them!

I'm definitely blocking each hexagon before sewing them all together. You could certainly block the blanket later and I imagine that the fabric squares would help the knitted hexagons keep their shape (especially if they're really made of fabric and not just cut up knitted sweaters like I'm planning). As for washing fabric and knitted hexagons together, I think you'd want to wash your fabric before cutting it and if you're worried about the knitted hexagons pre-wash them too before sewing. And I'd expect to have to block the blanket each time I wash it. It'll be almost all wool, so it won't be going through the dryer anyway. Since you have to lay it out to dry, it's just like blocking it.

So I'm guessing you're a little wary of this whole mishmash of textiles, huh? ;0)

Posted by: ALISON at February 4, 2008 4:07 PM

Oh, that made my head hurt! I'm glad that you figured it out, though.

Posted by: Sandy at February 4, 2008 4:18 PM

I love seeing math used for real world shtuff(rather than staid examples in books).

Posted by: Seanna Lea at February 4, 2008 5:33 PM

My eyes glazed over right about the third diagram. I can only assume you figured it out! Math and ames are unmixy things.

Posted by: ames at February 4, 2008 6:03 PM

Oooh, math! Love it. It all makes sense. :)

Posted by: Nikki at February 4, 2008 6:05 PM

You are a better person than I am. I would have just said, "Heck, it's a throw!", decided that 7" must be the diameter (point to point) and blithely gone on from there, figuring that since it was just a throw, that if I'd guessed wrong, I could always add on some more hexagons. (Of course, if I'd guessed wrong the wrong way and run out of yarn and fabric -- then, as EZ says in a different context, that is a vale of tears, make no mistake. Or something to that effect. Which would be my luck.)

Posted by: Cathy-Cate at February 4, 2008 6:43 PM

Call me crazy, but those sound like fun calculations! I love math and I love problem solving so I never grumble about having to break out the pencil and graph paper. I'm glad you got it all figured out and your blanket is going to be gorgeous!! I may need to go get that book too.

Posted by: Casey i at February 4, 2008 9:08 PM

i've been helping my son with his geometry, so it all made perfect sense!

Posted by: minnie at February 4, 2008 9:43 PM

Another math teacher chiming in here to say well done! I think I see a morning math problem about hexagons in my students' future!

Posted by: BethC at February 5, 2008 9:42 AM

If my brain wasn't fried from sleep, I would have followed. But, I love your pink hexagon.

Posted by: Amy at February 5, 2008 3:31 PM

I think my brain exploded. You lost me in the first paragraph. Math was never my friend. Not being diagnosed with ADD untill the 5th grade probably didn't help. Now my eyes glaze over whenever I hear the word "math". I really did try to understand your math-it almost made sense. Smells like progress.

Posted by: Erin at February 5, 2008 5:08 PM

Too much maths! But pretty hexagons. I can't wait to see more of the afghan.

Posted by: Kristin at February 6, 2008 4:22 AM